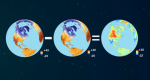
Bilineare Interpolation: Resample Image Cell Size with 4 Nearest Neighbors
Was ist bilineare Interpolation?
Wenn Sie Daten neu abtasten oder neu projizieren, müssen Sie möglicherweise Ihre Daten interpolieren.
Die gebräuchlichsten Resampling-Operatoren sind bilineare Interpolation, kubische Faltung und nächster Nachbar.
Heute konzentrieren wir uns auf die bilineare Interpolation, die eine Ausgangsfläche mit 4 bekannten Werten schätzt.
Wie unterscheidet sie sich von den anderen Interpolationsverfahren? Schauen wir uns das mal an.
Wann verwendet man bilineare Interpolation?
Bevor wir die bilineare Interpolation ausführlich erklären, ist es wichtig zu wissen, warum man sie überhaupt verwendet.
Temperaturgradientenraster, digitale Höhenmodelle, jährliche Niederschlagsraster, Rauschabstandsraster – das sind alles mögliche Beispiele dafür, wann Interpolation zur Neuabtastung von Bildern verwendet werden kann. Jedes Beispiel hat Werte, die kontinuierlich von Zelle zu Zelle variieren, um eine Oberfläche zu bilden.
Hier sind ein paar Beispiele dafür, wann Sie bilineare Interpolation verwenden würden:
- Wenn Sie Ihre Daten von einer Zellengröße auf eine andere umrechnen, ändern Sie die Zellengröße und benötigen eine Interpolation.
- Wenn Sie Ihre Rasterdaten auf ein anderes Koordinatensystem projizieren, ändern Sie die Konfiguration und nehmen eine Neuabtastung Ihrer Daten vor
In beiden Fällen würden Sie eine Neuabtastungstechnik verwenden. Denn wenn man ein Eingaberaster hat, woher weiß das Ausgaberaster, auf welchen Zellen die Ausgabe basieren soll, wenn die Eingabezellen nicht übereinstimmen?
Sie müssen ein Resampling-Verfahren wie z.B. bilineare Interpolation, kubische Faltung oder nächster Nachbar wählen.
Wie funktioniert die bilineare Interpolation
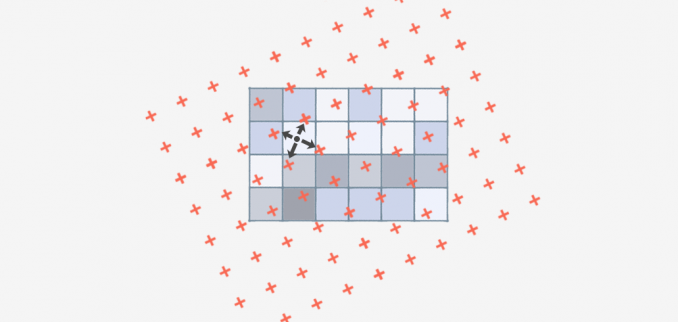
Die bilineare Interpolation ist eine Technik zur Berechnung von Werten einer Gitterposition auf der Grundlage benachbarter Gitterzellen. Der Hauptunterschied besteht darin, dass die VIER nächstgelegenen Zellzentren verwendet werden.
Die bilineare Interpolation verwendet die vier nächstgelegenen Nachbarzellen und ordnet den Wert der Ausgangszelle durch Bildung des gewichteten Durchschnitts zu. Die Gewichtung basiert auf dem Abstand der vier nächstgelegenen Zellzentren und glättet das Ausgaberaster.

Es wird empfohlen, die bilineare Interpolation für kontinuierliche Datensätze ohne klare Grenzen zu verwenden. Die Oberfläche muss kontinuierlich sein und die nächstgelegenen Punkte müssen miteinander in Beziehung stehen.
Wenn Sie den Prozess ausführen, erzeugt er eine glattere Oberfläche, die jedoch nicht so stark ist wie die kubische Faltung, die 16 benachbarte Zellen verwendet. Das Ausgaberaster nimmt nur die vier nächstgelegenen Zellzentren und wendet einen Mittelwert unter Verwendung des Abstands an.
Warum bilineare Interpolation?
Der Hauptunterschied bei der bilinearen Interpolation besteht darin, dass sie 4 nächste Nachbarn verwendet, um eine Ausgabefläche zu erzeugen.
Die kubische Faltung hingegen verwendet 16 nächste Nachbarn, wodurch die Oberfläche stärker geglättet wird.
Bilineare Interpolation setzt voraus, dass die Eingabe kontinuierlich ist.
Diese Resampling-Methode verwendet einen Abstandsmittelwert zur Schätzung, wobei näher gelegene Zellen höher gewichtet werden.