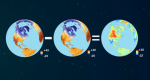
Interpolación Bilineal: Remuestrear el tamaño de la celda de la imagen con 4 vecinos más cercanos
¿Qué es la interpolación bilineal?
Cuando se remuestrean o reproyectan datos, es posible que haya que interpolarlos.
Los operadores de remuestreo más comunes son la interpolación bilineal, la convolución cúbica y el vecino más cercano.
Hoy nos centramos en la interpolación bilineal, que estima una superficie de salida con 4 valores conocidos.
¿En qué se diferencia de las otras técnicas de interpolación? Echemos un vistazo.
¿Cuándo se utiliza la interpolación bilineal?
Antes de que hagamos una explicación completa de la interpolación bilineal, es importante saber por qué se utilizaría en primer lugar.
Los rásteres de gradientes de temperatura, los modelos de elevación digital, las cuadrículas de precipitación anual, los rásteres de distancia de ruido – todos estos son ejemplos potenciales de cuando la interpolación se puede utilizar para remuestrear imágenes. Cada ejemplo tiene valores que varían continuamente de celda a celda para formar una superficie.
Aquí hay un par de ejemplos de cuándo se usaría la interpolación bilineal:
- Cuando remuestrea sus datos de un tamaño de celda a otro, está cambiando el tamaño de la celda y necesitaría interpolación.
- Cuando proyectas tus datos raster a otro sistema de coordenadas, estás cambiando la configuración y remuestreando tus datos
En ambos casos, utilizarías una técnica de remuestreo. Porque cuando tienes un raster de entrada, ¿cómo sabe el raster de salida en qué celdas basar la salida si las celdas de entrada no coinciden?
Tienes que seleccionar una técnica de remuestreo como la interpolación bilineal, la convolución cúbica o el vecino más cercano.
Cómo funciona la interpolación bilineal
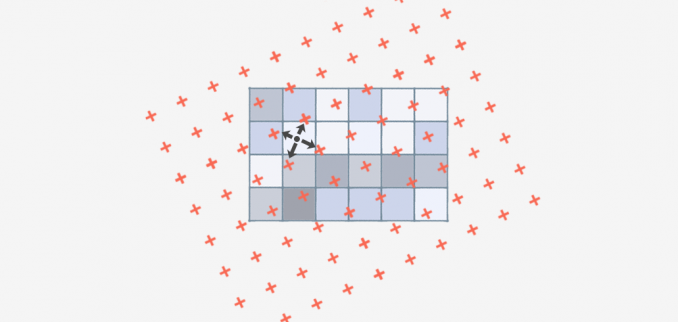
La interpolación bilineal es una técnica para calcular los valores de una ubicación de cuadrícula basada en las celdas de cuadrícula cercanas. La diferencia clave es que utiliza los CUATRO centros de celda más cercanos.
Usando las cuatro celdas vecinas más cercanas, la interpolación bilineal asigna el valor de la celda de salida tomando la media ponderada. Aplica pesos basados en la distancia de los cuatro centros de celda más cercanos suavizando la malla raster de salida.

Se recomienda utilizar la interpolación bilineal para conjuntos de datos continuos sin límites definidos. La superficie debe ser continua y los puntos más cercanos deben estar relacionados.
Cuando se ejecuta el proceso, genera una superficie más suave, pero no tan severa como la convolución cúbica que utiliza 16 celdas vecinas. El raster de salida tomará sólo cuatro centros de celdas más cercanos y aplicará un promedio utilizando la distancia.
¿Por qué utilizar la interpolación bilineal?
La diferencia clave en la interpolación bilineal es que utiliza 4 vecinos más cercanos para generar una superficie de salida.
Por otro lado, la convolución cúbica utiliza 16 vecinos más cercanos lo que suaviza más la superficie.
La interpolación bilineal asume que la entrada es continua.
Este método de remuestreo utiliza una media de distancia para estimar con las celdas más cercanas a las que se les da mayor peso.