Interpolacja bilinearna: Resample Image Cell Size with 4 Nearest Neighbors

Co to jest interpolacja bilinearna?

Podczas ponownego próbkowania lub reprojekcji danych może być konieczna interpolacja danych.

Najczęściej stosowanymi operatorami ponownego próbkowania są interpolacja bilinearna, konwolucja sześcienna i najbliższy sąsiad.

Dzisiaj skupimy się na interpolacji biliniowej, która szacuje powierzchnię wyjściową za pomocą 4 znanych wartości.

Czym różni się ona od innych technik interpolacji? Przyjrzyjmy się temu.

Kiedy używasz interpolacji bilinearnej?

Zanim zajmiemy się dogłębnym wyjaśnieniem interpolacji bilinearnej, ważne jest, aby wiedzieć, dlaczego można jej używać w pierwszej kolejności.

Rastry gradientów temperatury, cyfrowe modele wysokościowe, siatki rocznych opadów, raster odległości szumów – to wszystko są potencjalne przykłady, kiedy interpolacja może być używana do ponownego próbkowania obrazów. Każdy przykład ma wartości, które różnią się w sposób ciągły komórka do komórki, tworząc powierzchnię.

Oto kilka przykładów, kiedy można użyć interpolacji biliniowej:

• Gdy ponownie próbkujesz swoje dane z jednego rozmiaru komórki do innego, zmieniasz rozmiar komórki i potrzebujesz interpolacji.
• Gdy rzutujesz swoje dane rastrowe na inny układ współrzędnych, zmieniasz konfigurację i ponownie próbkujesz swoje dane

W obu tych przypadkach użyłbyś techniki ponownego próbkowania. Ponieważ kiedy masz raster wejściowy, skąd raster wyjściowy wie, na których komórkach oprzeć dane wyjściowe, jeśli komórki wejściowe nie pasują?

Musisz wybrać technikę resamplingu, taką jak interpolacja bilinearna, konwolucja sześcienna lub najbliższy sąsiad.

Jak działa interpolacja bilinearna

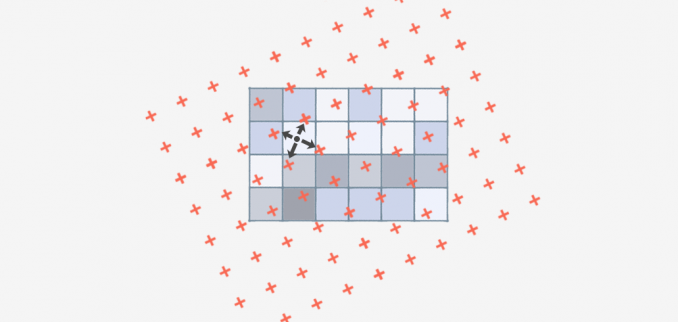
Interpolacja bilinearna to technika obliczania wartości położenia siatki na podstawie pobliskich komórek siatki. Kluczową różnicą jest to, że wykorzystuje ona CZTERY najbliższe centra komórek.

Używając czterech najbliższych sąsiednich komórek, interpolacja dwuliniowa przypisuje wartość komórki wyjściowej, biorąc średnią ważoną. Stosuje wagi na podstawie odległości czterech najbliższych ośrodków komórek, wygładzając wyjściową siatkę rastrową.

Zaleca się stosowanie interpolacji biliniowej w przypadku ciągłych zbiorów danych bez wyraźnych granic. Powierzchnia musi być ciągła, a najbliższe punkty muszą być ze sobą powiązane.

Po uruchomieniu procesu generuje on gładszą powierzchnię, ale nie tak surową jak konwolucja sześcienna, która wykorzystuje 16 sąsiadujących komórek. Raster wyjściowy pobierze tylko cztery najbliższe środki komórek i zastosuje średnią przy użyciu odległości.

Why Use Bilinear Interpolation?

Kluczową różnicą w interpolacji bilinearnej jest to, że używa ona 4 najbliższych sąsiadów do wygenerowania powierzchni wyjściowej.

Z drugiej strony, konwolucja sześcienna używa 16 najbliższych sąsiadów, co bardziej wygładza powierzchnię.

Interpolacja bilinearna zakłada, że dane wejściowe są ciągłe.

Ta metoda ponownego próbkowania używa średniej odległości do szacowania z bliższymi komórkami otrzymującymi wyższe wagi.

.

.