Die Entwicklung des Flächenmodells: Elementarstufe bis Algebra

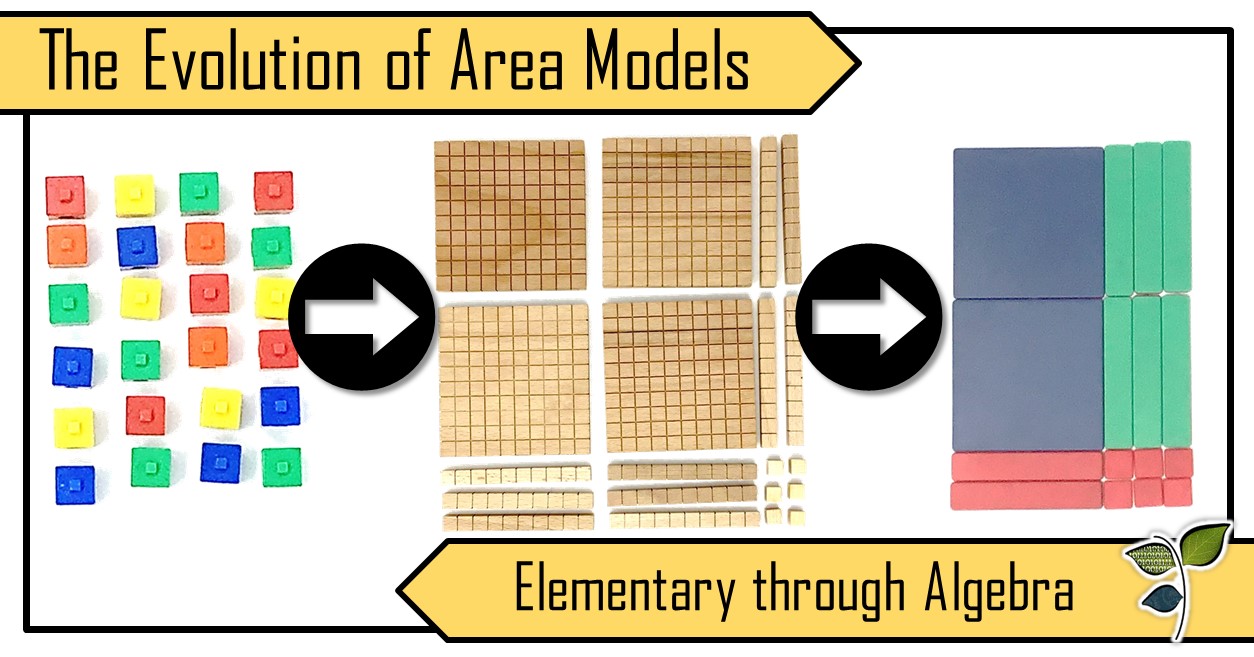
Wenn Kinder anfangen zu lernen, wie man Zahlen multipliziert, ist eines der ersten Dinge, die sie lernen, ein Muster mit Objekten in einer Reihe zu bilden. Sie zählen die Gegenstände und stellen fest, dass es eine Länge und eine Breite gibt. Sie können auch alle Manipulatoren zählen, um die Gesamtsumme zu ermitteln. Mit dieser frühen Erfahrung machen die Schüler einen ersten Schritt in Richtung einer Fähigkeit, die sie bis zur Highschool-Algebra ausbauen werden.

Als Common Core und andere Lehrpläne begannen, nicht standardisierte Algorithmen gegenüber den traditionellen Methoden zu betonen, die viele Erwachsene ausschließlich in der Schule verwendeten, gab es Gegenreaktionen. Überall tauchten Memes und Internet-Threads auf, die diese Nicht-Standard-Methoden als zu umständlich oder ineffizient abtaten. Sie verfehlten den Zweck des Lehrens und Lernens dieser Methoden, wie z. B. des Flächenmodells, für die mathematische Entwicklung unserer Schüler. Methoden wie Flächenmodelle werden mit dem Ziel entwickelt, ein dauerhaftes Verständnis für die Mechanik der Mathematik zu erlangen und nicht einfach nur die Antwort auf ein schnelles mathematisches Problem. Der Standardalgorithmus ist oft der effizienteste Weg, um ein Problem zu lösen, aber er verbirgt oft die mathematischen Überlegungen von Schülerinnen und Schülern, die in immer jüngeren Jahren lernen, kompliziertere Aufgaben zu lösen. Ja, das Flächenmodell sieht ganz anders aus als die Mathematik, die viele von uns als Kinder gemacht haben, aber die Mechanik ist die gleiche.

Flächenmodelle und -matrizen beruhen auf einem einfachen Gedanken: Die Länge eines Rechtecks mal seine Breite ist gleich der Gesamtfläche. Das erste Flächenmodell, das die Schülerinnen und Schüler verwenden, ist ein einfaches physikalisches Feld.

Dieses grundlegende Modell ist tatsächlich die Grundlage für das Lernen, das sich durch die gesamte Oberstufe zieht! Wie kann dieses Modell verwendet werden, um das Verständnis der jungen Schüler zu fördern? Der wichtigste Nutzen dieses Modells ist der visuelle Unterschied zwischen der Addition und der Multiplikation. Es verdeutlicht den Unterschied zwischen 6 + 4 und 6 x 4. Diese Unterscheidung wird sehr wichtig sein, wenn die SchülerInnen beginnen, die Reihenfolge der Operationen zu lernen. Sobald die Schüler die Multiplikationsfakten beherrschen, gehen sie zur zweistelligen Multiplikation über. Das ist der Punkt, an dem die Modelle eine Wendung nehmen, die vielen Erwachsenen Unbehagen bereitet!

Haben Ihre Schüler Schwierigkeiten, das physikalische Modell in den Algorithmus zu übernehmen? Versuchen Sie es mit diesem Tipp: Lassen Sie Ihre Schüler physikalische Anordnungen auf der Multiplikationstabelle aufbauen. Dies wird ihnen helfen, die Beziehung zwischen dem Modell, das sie bauen, und den Fakten, die sie gerade lernen, zu erkennen!

Die Verwendung von Manipulatoren wie Zehnerblöcken zur Darstellung von Stellenwertbeziehungen ist der nächste Schritt in der Entwicklung des Flächenmodells. Diese Methode kann für Pädagogen und Eltern schwierig sein, wenn sie nicht wissen, wie die Längen- und Breitenverhältnisse innerhalb der einzelnen Einheiten der Zehnerblöcke funktionieren. Ein weiterer Aspekt dieses Modells, der schwierig sein kann, ist die Fähigkeit der Blöcke, verschiedene Werte darzustellen. Bei der Multiplikation von ganzen Zahlen steht der Würfel für die Zahl eins, bei der Arbeit mit Dezimalzahlen steht der Würfel für ein Hundertstel. Die Modellierung des Stellenwerts zeigt den Schülern, warum bei der Multiplikation von 2 Ziffern mit 2 Ziffern eine Null gesetzt werden muss. Es kann auch Schülern, die weniger sicher mit der Multiplikation sind, eine Brücke geben, um von der 1-stelligen Multiplikation zu komplexeren Problemen zu gelangen.

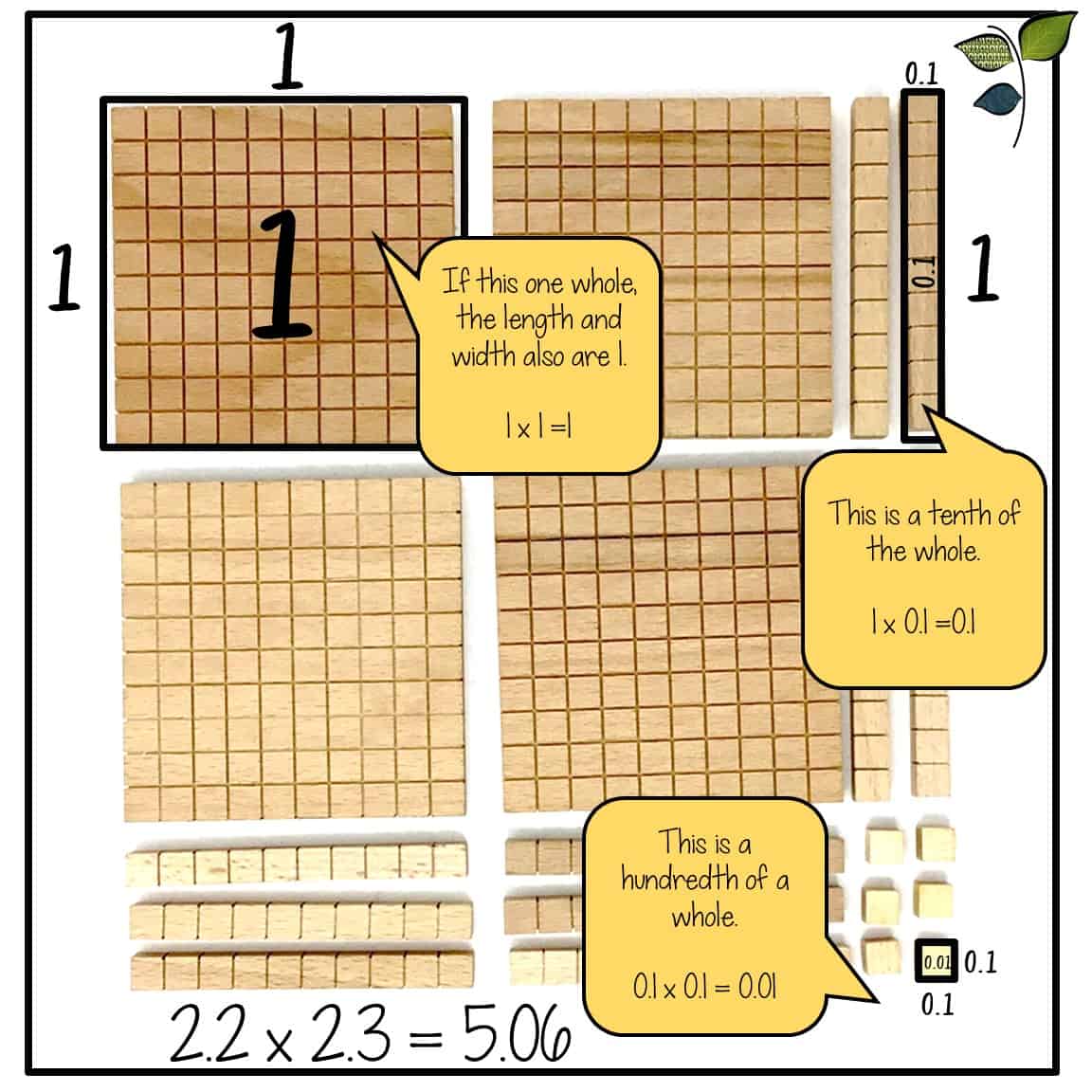
Wenn die Schüler etwa die fünfte oder sechste Klasse erreichen, nimmt die Verwendung von Flächenmodellen eine weitere Veränderung vor. Das konkrete Modell bewegt sich hin zu einer visuellen Darstellung. Bei Dezimalzahlen erfolgt dies häufig in Form eines Hunderterrasters. Die Verwendung dieses Modells ist eine der besten Möglichkeiten, um den Schülern zu vermitteln, warum Dezimalzahlen in einem Multiplikationsproblem nicht aneinandergereiht werden. Wenn die Schüler nur mit Algorithmen arbeiten, haben sie oft Schwierigkeiten, sich zu merken, wann Dezimalzahlen aufgereiht und wann sie verschoben werden müssen. Wenn man ihnen erklärt, warum die Dezimalstellen verschoben werden, können sie sich das Konzept besser einprägen und müssen sich nicht so stark auf das Auswendiglernen verlassen. Wenn die Schüler ein Flächenmodell zur Darstellung der Bruchmultiplikation verwenden, können sie sich auch den Grund für die Multiplikation der Nenner vorstellen. Nachdem sie gelernt haben, wie man Brüche addiert, ist dies wichtig, weil die Schülerinnen und Schüler die Idee, gemeinsame Nenner zu finden, als notwendig für die Arbeit mit Brüchen fest in ihr Gedächtnis eingeprägt haben. Beim Multiplizieren ist dies natürlich nicht erforderlich und führt zu einer falschen Antwort. Auch hier, wie bei der Arbeit mit Dezimalzahlen, sind viele Schüler verwirrt über die Regelunterschiede zwischen additiven und multiplikativen Operationen.

Haben Ihre Schüler Schwierigkeiten, die Länge und Breite in Dezimal- und Bruchflächenmodellen zu erkennen? Versuchen Sie diesen Tipp: Zeichnen Sie Zahlenlinien entlang der Länge und der Breite. Markieren Sie zuerst die Ganzzahlen. Markieren Sie dann die Ganzzahlen, um Einheitsquadrate zu bilden, damit der Nenner leicht gezählt werden kann. Schauen Sie sich das Video unten an, um die Schritte mit einer komplexen gemischten Zahlenmultiplikation zu sehen!

Alle vorherigen Modelle, auch wenn sie sich unterscheiden, befassen sich mit numerischen Längen und Breiten. Flächenmodelle müssen nicht mit numerischen Werten arbeiten und können zur Vereinfachung algebraischer Ausdrücke verwendet werden. Ein Manipulationsmittel namens Algebra-Kacheln wird häufig verwendet, um algebraische Flächenmodelle zu erstellen. Die Verwendung eines Flächenmodells zur Vereinfachung algebraischer Ausdrücke kann als Alternative zu FOIL verwendet werden. Obwohl viele von uns, die jetzt unterrichten, mit der FOIL-Methode aufgewachsen sind, einer Eselsbrücke, die für first, outside, inside, last steht, um algebraische Ausdrücke zu multiplizieren, hat diese Methode einige offensichtliche Mängel. Einer der größten ist, wenn eine der Klammern drei Terme anstelle von zwei enthält. Die FOIL-Methode funktioniert nur, wenn beide Multiplikatoren nur zwei Terme haben, aber es gibt nichts, was algebraische Probleme auf zwei Terme begrenzt. Schüler, die keine andere Methode als die FOIL-Methode kennen, werden wahrscheinlich bei einem Problem stecken bleiben, wenn sie keine andere Methode anwenden können.

Flächenmodelle sind ein wesentliches Hilfsmittel, um das Verständnis multiplikativer Beziehungen zu vertiefen. Von der ersten Verwendung zum Aufbau von Multiplikationsfakten bis hin zur Algebra sind diese Modelle, obwohl sie nicht das sind, womit die meisten von uns aufgewachsen sind, als wir selbst Mathematik lernten, eine der besten Methoden, um ein konstantes und verständliches Modell für das Verständnis der Schüler zu schaffen. Auch wenn die Mathematik immer komplexer wird, kann jedes Mal das Gefühl vermittelt werden, dass es sich um etwas bereits Bekanntes handelt, indem ein vertrautes Lösungsmodell verwendet wird.