Bilineaarinen interpolointi:
Mitä on bilineaarinen interpolointi?
Kun otat uudelleen näytteitä tai projisoit tietoja, saatat joutua interpoloimaan tietosi.
Yleisimmät uudelleen näytteenotto-operaattorit ovat bilineaarinen interpolointi, kuutiollinen konvoluutio ja lähin naapuri.
Tänään keskitymme bilineaariseen interpolointiin, joka estimoi tulostuspintaa neljällä tunnetulla arvolla.
Miten se eroaa muista interpolointitekniikoista? Katsotaanpa.
Milloin käytät bilineaarista interpolointia?
Ennen kuin selitämme bilineaarisen interpoloinnin perusteellisesti, on tärkeää tietää, miksi sitä ylipäätään käytetään.
Lämpötilagradienttirasterit, digitaaliset korkeusmallit, vuotuiset sademääräruudukot, kohinan etäisyysrasterit – nämä kaikki ovat mahdollisia esimerkkejä siitä, milloin interpolointia voidaan käyttää kuvien uudelleennäytteenottoon. Jokaisessa esimerkissä on arvoja, jotka vaihtelevat jatkuvasti solusta toiseen muodostaen pinnan.
Tässä on pari esimerkkiä siitä, milloin voit käyttää bilineaarista interpolointia:
- Kun otat datan uudelleen näytteenottoa solukoolta toiselle, muutat solukokoa ja tarvitsisit interpolointia.
- Kun projisoit rasteridatan toiseen koordinaattijärjestelmään, muutat konfiguraatiota ja otat datan uudelleen näytteenottoa
Kummassakin näistä tapauksista käyttäisit uudelleen näytteenottotekniikkaa. Koska kun sinulla on syöttörasteri, miten lähtörasteri tietää, mihin soluihin tulostus perustuu, jos syöttösolut eivät vastaa toisiaan?
Sinun on valittava uudelleen näytteenottotekniikka, kuten bilineaarinen interpolointi, kuutiomainen konvoluutio tai lähin naapuri.
Miten bilineaarinen interpolointi toimii
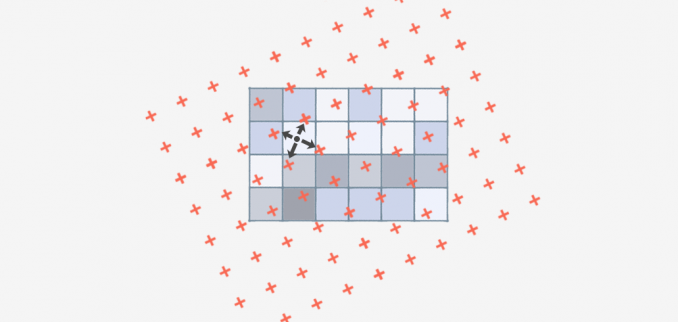
Bilineaarinen interpolointi on tekniikka, jolla lasketaan ruudukon sijainnin arvot läheisten ruudukon solujen perusteella. Keskeinen ero on se, että siinä käytetään NELJÄÄ lähintä solukeskipistettä.
Käyttäen neljää lähintä naapurisolua bilineaarinen interpolointi määrittää lähtösolun arvon ottamalla painotetun keskiarvon. Se käyttää painoja neljän lähimmän solukeskuksen etäisyyden perusteella tasoittaen tulostusrasterin.

Bilineaarista interpolointia suositellaan käytettäväksi jatkuviin tietokokonaisuuksiin, joissa ei ole selviä rajoja. Pinnan on oltava jatkuva ja lähimpien pisteiden on liityttävä toisiinsa.
Kun suoritat prosessin, se tuottaa tasaisemman pinnan, mutta ei yhtä ankaran kuin kuutiollinen konvoluutio, joka käyttää 16 naapurisolua. Lähtörasteri ottaa vain neljä lähintä solukeskipistettä ja soveltaa keskiarvoa etäisyyden avulla.
Miksi käyttää bilineaarista interpolointia?
Keskeinen ero bilineaarisessa interpoloinnissa on se, että se käyttää neljää lähintä naapuripistettä tulostuspinnan tuottamiseen.
Toisaalta kuutiollinen konvoluutio käyttää 16 lähintä naapuripistettä, mikä tasoittaa pintaa enemmän.
Bilineaarinen interpolointi olettaa, että tuloarvo on jatkuva.
Tämä uudelleen näytteenottomenetelmä käyttää etäisyyskeskiarvoa estimointiin, jossa lähempänä oleville soluille annetaan suuremmat painot.