エリアモデルの進化。 Elementary through Algebra

子どもたちが数の掛け算を学び始めるとき、最初に学ぶことの1つは、配列にあるオブジェクトでパターンを作ることである。 マニピュレータを数えて、長さと幅があることに気づきます。 また、すべてのマニピュレーターを数えて、合計を求めることもできます。

コモンコアや他のカリキュラムが、多くの大人が学校で独占的に使っていた伝統的な方法よりも、非標準のアルゴリズムを強調し始めたとき、反発があった。 このような非標準的な手法を過度に煩雑であったり非効率的であったりするとして非難することに専念するミームやインターネット上のスレッドがいたるところに出現したのです。 これらは、生徒の数学的発達における面積モデルのようなこれらの方法の指導と学習の目的を見逃していました。 面積モデルのような方法は、単に手っ取り早く数学の問題の答えを得るのではなく、数学の仕組みを永続的に理解する目的で開発されたものです。 標準的なアルゴリズムは、問題を解くのに最も効率的な方法であることが多いですが、低年齢でより複雑な作業を学ぶ生徒から数学の理屈を隠してしまうことがよくあります。 そう、面積モデルは、私たちの多くが子供の頃にやった算数と非常に違って見えますが、仕組みは同じです。

面積モデルと配列は、長方形またはその幅の倍が合計面積に等しくなるという、1 つの単純な思考に依存しています。 生徒が最初に使う面積モデル・モデルは、単純な物理的配列である。

この基本モデルは、実は高校まで続く学習の基礎となるのだ! このモデルは、若い生徒の理解をさらに深めるためにどのように使うことができるでしょうか。 このモデルの最も重要な使い方は、掛け算と比較して足し算がどのようなものであるかの視覚的な違いです。 この違いは、生徒が操作の順序を学習し始めたときに非常に重要になります。 掛け算の基本をマスターしたら、次は2桁の掛け算です。 ここで、多くの大人が数学に違和感を持ち始めるという展開になります！

生徒が物理モデルをアルゴリズムに取り込むのに苦労していませんか？ このヒントを試してみてください：生徒たちに、乗算表の上に物理的な配列を作らせます。 これは、彼らが構築しているモデルと彼らが学習に取り組んでいる事実との関係を見るのに役立ちます！

場所値の関係を示すために基礎10ブロックなどの操作手段を使用することは、面積モデルの進化の次のステップである。 この方法は、10ブロックの各単位の中で長さと幅の関係がどのように働くかに慣れていない教育者や親にとって、厄介なものになる可能性があります。 このモデルのもう一つの難しい点は、ブロックが異なる値を表すことができることです。 整数の掛け算の場合、単位立方体は1を表しますが、小数の場合、単位立方体は100分の1を表します。 2桁と2桁の掛け算をするときに、なぜゼロを置かなければならないかを、場所価値のモデルを使って生徒に示すことができます。 また、掛け算にあまり自信のない生徒に、1桁の掛け算からより複雑な問題への橋渡しをすることができます。

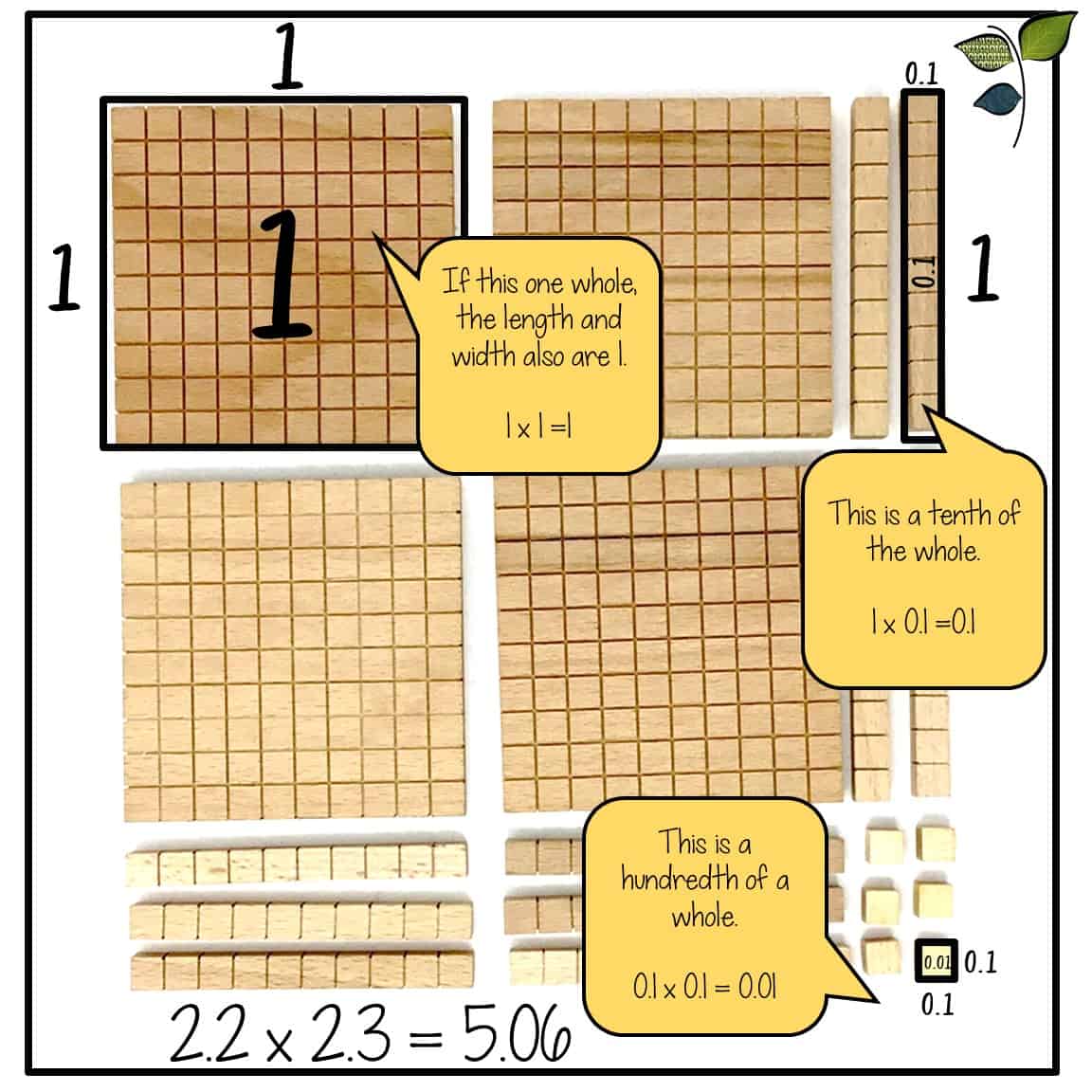
5年生か6年生くらいになると、面積モデルの使用は別の変化を遂げます。 具体的なモデルは、視覚的な表現に移行します。 小数の場合、これはしばしば百のグリッドの形をとります。 このモデルを使うことは、掛け算の問題でなぜ小数が並ばないかを理解させる最も良い方法の一つである。 アルゴリズム学習しかしていない生徒は、小数を並べるときと動かすときのタイミングがうまく覚えられないことがよくあります。 小数を並べる理由を理解させることで、より自然な記憶と理解を得ることができ、暗記に頼ることも少なくなるはずです。 また、分数の掛け算を面積モデルで表現すると、分母の掛け算の理由を視覚的に理解することができます。 分数の足し算を学んだ後、分数を扱う上で必要な共通分母を求めるという考え方をしっかりと頭に叩き込んでいるため、この点は重要です。 掛け算の場合、もちろんこれは必要なく、間違った答えになります。

小数と分数の面積モデルで、長さと幅を見るのに苦労していませんか？ このヒントを試してみてください：長さと幅に沿って数列を描きます。 まず、全体像に印をつける。 次に、分母を数えやすいように、分母をハイライトして単位マスを作ります。 下のビデオで、複雑な混合数の掛け算を使った手順をご覧ください！

これまでのモデルはすべて、違いはあっても、長さと幅の数字を扱ったものでした。 面積モデルは数値を使う必要がなく、代数的な式を簡略化するために使うことができる。 代数的な面積モデルを作るには、代数タイルと呼ばれるマニピュレータがよく使われる。 面積モデルを用いて代数的な式を簡略化することは、FOILの代わりとして用いることができる。 FOILはfirst, outside, inside, lastの頭文字をとった略語で、代数式の掛け算をするために使われてきたが、この方法にはいくつかの欠点がある。 その一つは、括弧の中に2項ではなく3項が含まれている場合である。 FOIL法は両方の乗法が2項しかない場合にのみ有効であるが、代数的問題を2項に限定するようなことは何もない。 FOIL以外の方法がない学生は、他の方法がない問題で行き詰まる可能性が高い。

面積モデルは乗法関係を完全に理解するために不可欠なツールである。 掛け算の事実を構築するための最初の使用から、代数まで、このモデルは、自分自身が数学を学ぶときに育ったものではありませんが、学生のための理解の一定かつ理解しやすいモデルを作成するための最良の方法の 1 つです。

。