The Evolution of the Area Model: Elementary through Algebra

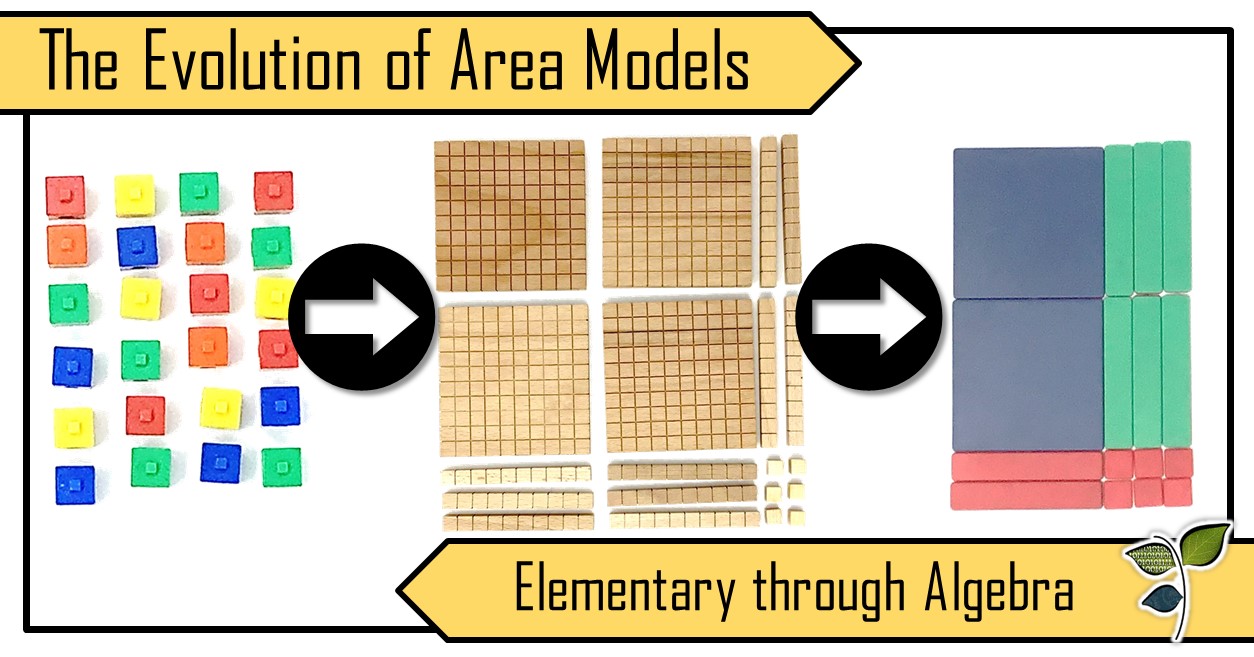
Wanneer kinderen beginnen te leren hoe ze getallen moeten vermenigvuldigen, is een van de eerste dingen die ze leren een patroon te maken met voorwerpen in een matrix. Ze tellen de manipulatieven en merken op dat er een lengte en een breedte is. Dat ze ook alle manipulatieven kunnen tellen om een totaal te vinden. Vanuit deze vroege ervaring, studenten beginnen een eerste stap in de richting van een vaardigheid die zal blijven bouwen helemaal tot de middelbare school algebra.

Toen Common Core en andere curricula begon te benadrukken niet-standaard algoritmen in plaats van de traditionele methoden die veel volwassenen gebruikten uitsluitend op school, was er backlash. Memes en internet threads gewijd aan het slamming van deze niet-standaard methoden als te omslachtig of inefficiënt dook overal op. Deze gingen voorbij aan het doel van het onderwijzen en leren van deze methoden, zoals het oppervlaktemodel in de wiskundige ontwikkeling van onze leerlingen. Methoden zoals oppervlaktemodellen zijn ontwikkeld met het doel om een blijvend begrip te krijgen van de mechanica van de wiskunde in plaats van alleen maar het antwoord op een snel wiskundeprobleem. Het standaardalgoritme is vaak de meest efficiënte manier om een probleem op te lossen, maar het verbergt vaak de redenering van de wiskunde voor leerlingen die op steeds jongere leeftijd meer ingewikkeld werk leren doen. Ja, het oppervlaktemodel ziet er heel anders uit dan de wiskunde die velen van ons als kind deden, maar de mechanica is hetzelfde.

Area-modellen en arrays berusten op één eenvoudige gedachte: de lengte of een rechthoek maal de breedte zal gelijk zijn aan de totale oppervlakte. Het eerste oppervlaktemodel dat leerlingen gebruiken is een eenvoudige fysieke matrix.

Dit basismodel is in feite de basis voor het leren dat de hele middelbare school doorgaat! Hoe kan dit model worden gebruikt om het begrip van jonge leerlingen te bevorderen? Het belangrijkste gebruik van dit model is het visuele verschil tussen hoe optellen eruit ziet in vergelijking met vermenigvuldigen. Het maakt duidelijker hoe verschillend 6 + 4 is van 6 x 4. Dit onderscheid zal heel belangrijk zijn wanneer de leerlingen de volgorde van bewerkingen beginnen te bestuderen. Zodra de leerlingen de vermenigvuldigingsfeiten onder de knie hebben, gaan ze verder met vermenigvuldigen met twee cijfers. Dit is waar de modellen de wending nemen die veel volwassenen ongemakkelijk beginnen te vinden!

Hebben uw leerlingen moeite om het fysieke model mee te nemen in het algoritme? Probeer deze tip eens: laat uw leerlingen fysieke reeksen bouwen bovenop het vermenigvuldigingstabel. Dit zal hen helpen het verband te zien tussen het model dat ze bouwen en de feiten die ze aan het leren zijn!

Het gebruik van manipulatieven zoals basistienblokjes om plaatswaarde-relaties te laten zien, is de volgende stap in de evolutie van het gebiedsmodel. Deze methode kan lastig zijn voor opvoeders en ouders die niet gewend zijn aan hoe de lengte- en breedteverhoudingen werken binnen elk van de eenheden van de basistienblokken. Een ander aspect van dit model dat moeilijk kan zijn, is de mogelijkheid van de blokken om verschillende waarden voor te stellen. Bij vermenigvuldiging met gehele getallen staat de eenheidsblok voor één, maar bij decimalen staat de eenheidsblok voor een honderdste. Het gebruik van plaatswaarde modellering laat leerlingen zien waarom een nul moet worden geplaatst bij het vermenigvuldigen van 2-cijfers met 2-cijfers. Het kan leerlingen die minder vertrouwen hebben in vermenigvuldigen ook een brug geven om van een ééncijferige vermenigvuldiging naar complexere problemen te komen.

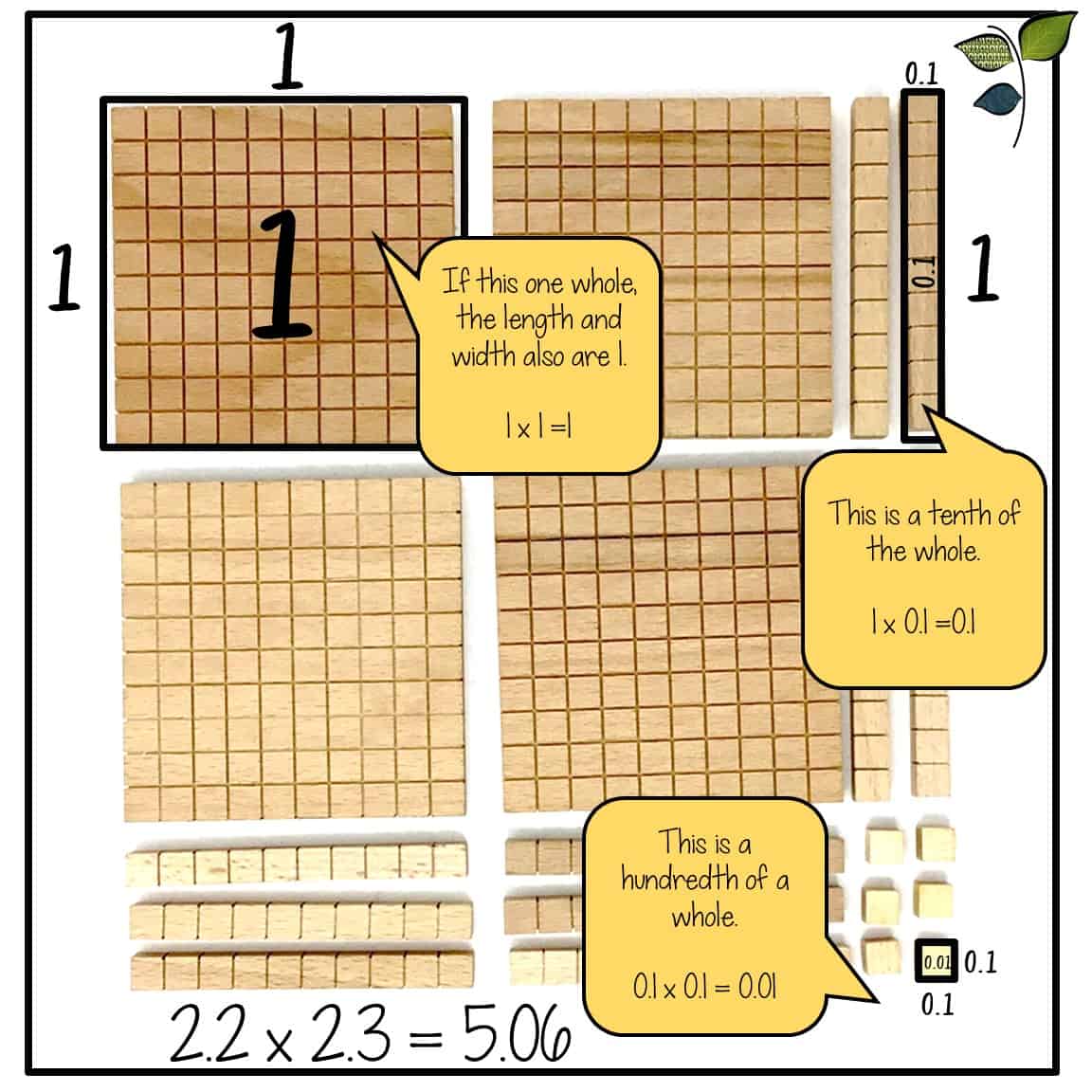
Als leerlingen eenmaal in groep 5 of 6 zitten, ondergaat het gebruik van oppervlaktemodellen een andere gedaanteverandering. Het concrete model gaat over in een visuele voorstelling. Bij decimalen neemt dit vaak de vorm aan van een honderdtallig rooster. Het gebruik van dit model is een van de beste manieren om leerlingen te laten begrijpen waarom decimalen niet op een rij staan in een vermenigvuldigingsprobleem. Als leerlingen alleen met algoritmen werken, hebben ze vaak moeite te onthouden wanneer ze decimalen op een rij moeten zetten en wanneer ze een decimaal moeten verplaatsen. Door hen te laten begrijpen waarom decimalen op een rij moeten worden gezet, zullen ze het concept op een natuurlijker manier onthouden en het minder snel uit het hoofd hoeven te leren. Als de leerlingen een oppervlaktemodel gebruiken om de vermenigvuldiging van breuken voor te stellen, kunnen ze ook de reden voor de vermenigvuldiging van de noemers visualiseren. Na het leren optellen van breuken is dit belangrijk omdat de leerlingen het idee van het vinden van gemeenschappelijke noemers stevig in hun geheugen hebben geplant als noodzakelijk voor het werken met breuken. Bij vermenigvuldigen is dit natuurlijk niet nodig en zal het tot een verkeerd antwoord leiden. Net als bij het werken met decimalen raken veel leerlingen in de war over de regelverschillen tussen additieve en multiplicatieve bewerkingen.

Hebben uw leerlingen moeite met het zien van de lengte en breedte in decimale en breukvlakmodellen? Probeer deze tip eens: trek getallenlijnen langs de lengte en de breedte. Markeer eerst de gehelen. Markeer vervolgens de gehelen om eenheidsvierkanten te maken, zodat de noemer gemakkelijk geteld kan worden. Bekijk de video hieronder om de stappen te zien met een complexe vermenigvuldiging van gemengde getallen!

Alle voorgaande modellen, hoewel verschillend, hebben te maken met numerieke lengte en breedte. Oppervlaktemodellen hoeven geen numerieke waarden te gebruiken en kunnen worden gebruikt om algebraïsche uitdrukkingen te vereenvoudigen. Een manipulatief genaamd algebra tegels worden vaak gebruikt om algebraïsche gebiedsmodellen te bouwen. Het gebruik van een oppervlaktemodel om algebraïsche uitdrukkingen te vereenvoudigen kan worden gebruikt als een alternatief voor FOIL. Hoewel velen van ons die nu lesgeven zijn opgegroeid met het gebruik van de FOIL-methode, een geheugensteuntje dat staat voor first, outside, inside, last, om algebraïsche uitdrukkingen te vermenigvuldigen, heeft deze methode enkele duidelijke tekortkomingen. Een van de grootste is wanneer een van de haakjes drie termen bevat in plaats van twee. De FOIL-methode werkt alleen als beide vermenigvuldigers slechts twee termen hebben, maar er is niets dat algebraïsche problemen beperkt tot twee termen. Leerlingen die geen andere methode dan FOIL hebben, zullen waarschijnlijk vastlopen op een probleem dat ze niet kunnen gebruiken.

Gebiedsmodellen zijn een essentieel hulpmiddel om het begrip van vermenigvuldigingsrelaties te vervolledigen. Vanaf het eerste gebruik om vermenigvuldigingsfeiten op te bouwen tot en met algebra is dit model, hoewel het niet het model is waarmee de meesten van ons zijn opgegroeid toen ze zelf wiskunde leerden, een van de beste methoden om een constant en begrijpelijk model van begrip voor leerlingen te creëren. Hoewel de wiskunde steeds complexer wordt, kan het telkens het gevoel geven dat het iets is dat al bekend is door een vertrouwd model van oplossen te gebruiken.