The Evolution of the Area Model: The Evolution of the Area Model: Elementary through Algebra

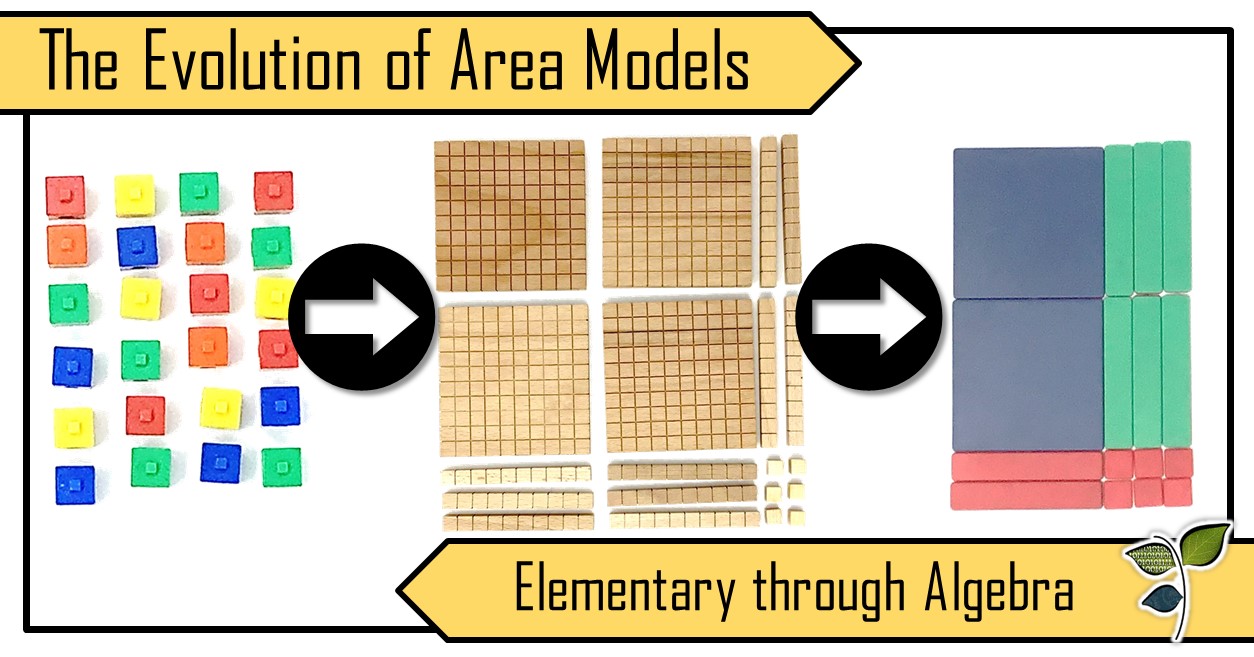
Når børn begynder at lære at gange tal, er en af de første ting, de lærer, at lave et mønster med genstande i en række. De tæller de manipulerede genstande og bemærker, at der er en længde og en bredde. At de også kan tælle alle manipulativerne for at finde en total. Fra denne tidlige erfaring begynder eleverne et første skridt mod en færdighed, der vil fortsætte med at blive opbygget hele vejen gennem algebra i gymnasiet.

Da Common Core og andre læseplaner begyndte at lægge vægt på ikke-standardiserede algoritmer frem for de traditionelle metoder, som mange voksne udelukkende brugte i skolen, var der modreaktioner. Memes og internettråde, der var dedikeret til at smadre disse ikke-standardiserede metoder som overdrevent besværlige eller ineffektive, dukkede op overalt. Disse gik glip af formålet med undervisningen i og indlæringen af disse metoder, som f.eks. arealmodellen i vores elevers matematiske udvikling. Metoder som f.eks. arealmodeller er udviklet med det formål at opnå en varig forståelse af matematikkens mekanik snarere end blot at få svar på et hurtigt matematikopgave. Standardalgoritmen er ofte den mest effektive måde at løse et problem på, men den skjuler ofte den matematiske tankegang for elever, der lærer at udføre mere kompliceret arbejde i en stadig yngre alder. Ja, arealmodellen ser meget anderledes ud end den matematik, som mange af os lavede som børn, men mekanikken er den samme.

Arealmodeller og arrays bygger på én simpel tanke: længden eller et rektangel gange dets bredde vil være lig med det samlede areal. Den første arealmodelmodel, som eleverne bruger, er et simpelt fysisk array.

Denne grundlæggende model er faktisk grundlaget for den læring, der fortsætter gennem gymnasiet! Hvordan kan denne model bruges til at fremme de unge elevers forståelse? Den vigtigste anvendelse af denne model er den visuelle forskel mellem, hvordan addition ser ud i forhold til multiplikation. Den gør det mere tydeligt, hvor forskelligt 6 + 4 er fra 6 x 4. Denne forskel vil være meget vigtig, når eleverne begynder at studere rækkefølgen af operationer. Når eleverne har behersket multiplikationsfakta, går de videre til tocifret multiplikation. Det er her, modellerne tager den drejning, som mange voksne begynder at blive utrygge ved matematikken!

Har dine elever problemer med at tage den fysiske model med ind i algoritmen? Prøv dette tip: Lad dine elever bygge fysiske arrays oven på multiplikationsskemaet. Dette vil hjælpe dem med at se sammenhængen mellem den model, de bygger, og de fakta, de arbejder på at lære!

Anvendelse af manipulatorer som base ti-blokke til at vise stedværdisammenhænge er det næste skridt i udviklingen af arealmodellen. Denne metode kan være vanskelig for pædagoger og forældre, som ikke er vant til, hvordan længde- og breddeforholdet fungerer inden for hver af enhederne i base ti-klodserne. Et andet aspekt af denne model, der kan være vanskeligt, er klodsenes evne til at repræsentere forskellige værdier. Når der arbejdes med multiplikation med hele tal, repræsenterer enhedskubben én, men når der arbejdes med decimaltal, repræsenterer enhedskubben en hundrededel. Ved at bruge stedværdimodellering viser eleverne, hvorfor der skal placeres et nul, når tocifrede tal ganges med tocifrede tal. Det kan også give elever, der er mindre sikre på multiplikation, en bro til at komme fra 1-cifret multiplikation til mere komplekse problemer.

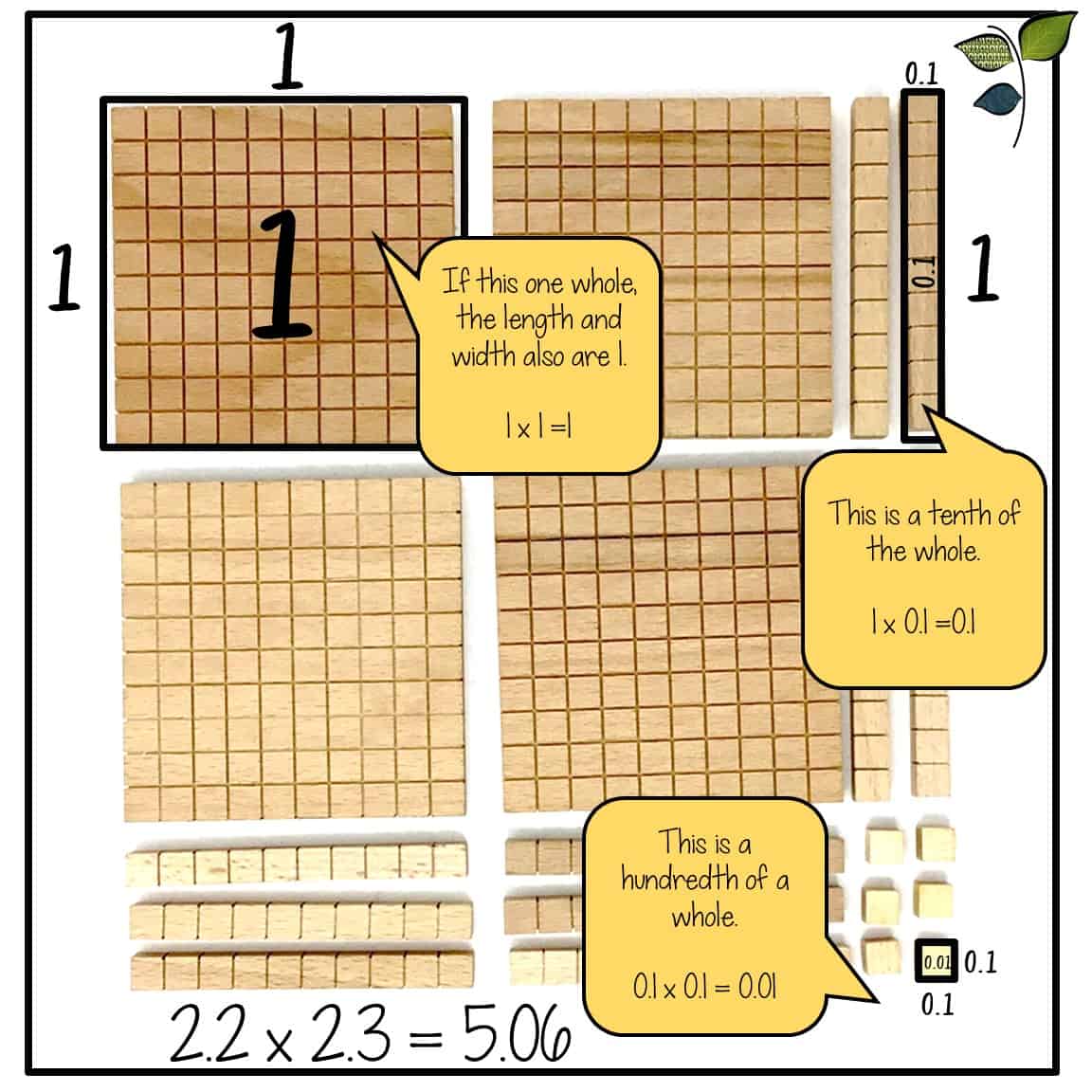
Når eleverne når omkring femte eller sjette klasse, tager brugen af arealmodeller en anden forvandling. Den konkrete model bevæger sig i retning af en visuel repræsentation. Med decimaltal tager dette ofte form af et hundredegitter. Brug af denne model er en af de bedste måder at give eleverne forståelse for, hvorfor decimaltal ikke står på række i et multiplikationsopgave. Når eleverne kun udsættes for algoritmearbejde, har de ofte problemer med at huske, hvornår decimaler skal stilles på linje i forhold til, hvornår et decimaltal skal flyttes. Hvis man giver dem forståelse for hvorfor decimalplacering vil det hjælpe dem til at få en mere naturlig hukommelse og forståelse af begrebet, og de vil ikke skulle stole så meget på udenadslære. Når eleverne bruger en arealmodel til at repræsentere brøkmultiplikation, er de også i stand til at visualisere årsagen til multiplikationen af nævnerne. Efter at have lært at addere brøker er dette vigtigt, fordi eleverne har fået indprentet ideen om at finde fællesnævnere i deres hjerne som nødvendig for at arbejde med brøker. Ved multiplikation er dette naturligvis ikke nødvendigt, og det vil resultere i et forkert svar. Igen, ligesom når man arbejder med decimaltal, bliver mange elever forvirrede over regelforskellene mellem additive og multiplikative operationer.

Har dine elever problemer med at se længden og bredden i decimale og brøkformede arealmodeller? Prøv dette tip: Tegn tallinjer langs længden og bredden. Marker først helhederne. Marker derefter helhederne for at lave enhedsfirkanter, så nævneren nemt kan tælles. Se videoen nedenfor for at se trinene med en kompleks multiplikation med blandede tal!

Alle de foregående modeller, selv om de er forskellige, omhandler numerisk længde og bredde. Arealmodeller behøver ikke at bruge numeriske værdier og kan bruges til at forenkle algebraiske udtryk. Et manipuleringsmiddel kaldet algebrafliser bruges almindeligvis til at bygge algebraiske arealmodeller. Anvendelse af en arealmodel til forenkling af algebraiske udtryk kan bruges som et alternativ til FOIL. Selv om mange af os, der underviser nu, er vokset op med FOIL-metoden, en mnemoteknik, der står for first, outside, inside, last, til at multiplicere algebraiske udtryk, har denne metode nogle åbenlyse mangler. En af de største er, når en af parenteserne indeholder tre termer i stedet for to. FOIL-metoden virker kun, hvis begge multiplikatorer kun har to termer, men der er intet, der begrænser algebraiske problemer til to termer. Elever, der ikke har nogen anden metode end FOIL, vil sandsynligvis sidde fast på et problem uden nogen anden metode at bruge.

Area-modeller er et vigtigt redskab til at fylde forståelse af multiplikative sammenhænge. Fra den første brug til at opbygge multiplikationsfakta hele vejen gennem algebra er denne model, selv om den ikke er det, de fleste af os er vokset op med, da vi selv lærte matematik, en af de bedste metoder til at skabe en konstant og forståelig model for forståelse for eleverne. Selv om matematikken bliver mere kompleks, kan man hver gang få det til at føles som om, at det er noget, man allerede kender ved at bruge en velkendt løsningsmodel.